Long Term Savings – the need to start early
Saving for income in retirement can be a daunting thought for most people – the problem they face is that they simply don’t know how much they need to save between now and retirement.
In this article we consider the time value of money, and in particular, the benefits to be enjoyed from “compound growth”. In later articles we consider just how you go about working out how much you need to invest to plan for your own retirement income.
The Rule of 72
In the article “The Rule of 72 – the Time Value of Money” we discussed a simple technique for calculating how your money grows over time whereby dividing the rate of growth you are enjoying on your money into 72 shows the number of years it takes for your money to double in value.
For example – if you were lucky enough to receive 6% annual interest on your money in a savings account then this would double in value every 12 years (72/6=12).
Compound Interest
The principle of compound interest is simply one of “money makes money”. An example of this would be investing £100 in a savings account at 10% interest – after one year your money would have grown to £110 – after two years, £121 – you have earned an extra £1 interest in year two as not only have you earned 10% on your original investment of £100 but you have also earned 10% interest on the £10 interest you made in year one and this continues for as long as you leave that money invested.
Over time, as the proportion of “interest earned” grows then the rate at which your overall investment grows also increases – it’s like a snowball effect – when you roll a small snowball down a hill at first it grows slowly – the more it rolls, the more snow it picks up on each rotation and the faster it moves…….
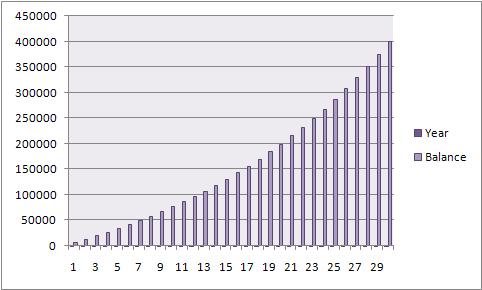
The following chart shows how £500 per month, enjoying a simple return of 5% per annum, grows over a 30 year period –
The above chart shows that in the earlier years the rate of growth on the funds invested is relatively low, and as the benefits of compound growth accumulate over time the curve of the graph becomes steeper as each and every £1 of interest earned subsequently earns its own interest!
It’s not how much you save, but how long….
The principle of compound interest therefore brings us nicely into the subject of pension planning, saving for retirement or any other form of long-term saving.
For the sake of this example we will consider that you wish to retire at age 60 and you are now aged 30.
You have calculated that to provide income in retirement of £20,000 per year, ignoring inflation for the time being, and assuming a return of 5% after charges for both the growth on your money being invested BEFORE retirement and for the annuity income you receive AFTER retirement, that to provide £20,000 per annum you need a fund of £400,000 (£20,000 per annum divided by 0.05).
So to achieve this income goal you need to build up a fund between now and retirement of £400,000. Logic says that we simply divide the fund needed between the number of years to retirement and this tells us how much we need to save each year – in this example £400,000 over 30 years requires a saving of £13,333.33 per year (£1,111.11 per month)
This however doesn’t take into account the growth that you would enjoy on each contribution being paid into the investment vehicle – the contribution made in month 1 would have the longest time to grow – 29 years and 11 months, the contribution made in month 2 – 29 years and 10 months and so on…….
Compound Growth and Regular Savings
Saving on a regular basis into an asset-backed investment, such as a pension fund, or a unit trust held under an ISA umbrella, can benefit from “pound cost averaging”. In a volatile stock market, such as the one we are currently in, investing on a regular monthly basis means that you effectively have 12 chances each year to invest some of your money into the stock market on a day when the market is lower than on other days. The benefit of this is that it brings down the average cost of the units you hold, and ultimately leads to a larger potential profit at the end.
In our example above we calculated the monthly contribution required to build a fund of £400,000 assuming no growth
If we add in say net annual growth of 5% after charges (which should be achievable over the medium to long term) then the monthly investment actually falls to £480.62 per month.
If the rate of growth increases to say 6% per year, the monthly investment falls to £398.20 per month.
If the rate of growth again increases to say 9%, the monthly investment required to hit £400,000 falls to £218.49.
The Cost of Delay
Above we calculated that £480.62 invested at 5% net per annum will grow to £400,000 over a 30 year period. If we reduce the term to 29 years, then to achieve the same fund value, the monthly investment needs to be £512.77 per month – an additional monthly investment of £32.15 or an additional total investment of £11,188.20 over the life of the investment. This shows the cost of delay.
So by waiting one year, an additional £32.15 per month needs to be invested, each and every month for the whole 29 year period, to provide the same £400,000 fund at age 60.
If the individual were to delay their regular savings by 2 years then a monthly investment of £547.63 would be needed – delay by just 5 years and the monthly contribution rises to £671.69 which is probably beyond the means of most families with average income and outgoings.
Starting Early
We have now calculated that the regular saving to build a fund of £400,000 over 30 years, at 5% net return per annum, would be £480.62 per month – but what if you were to start earlier?
If you had the foresight to have started last year, and therefore have a period of 31 years over which to make this investment then this monthly investment would fall to £450.90 – start 5 years earlier and the monthly investment would need to be £352.08……………….
Conclusion
In conclusion then it is vitally important that you start saving as soon as possible for retirement income – whether that be through a personal pension, stocks and shares ISA, a deposit account…….
Start as soon as possible!
Ask yourself this question – how many more paydays until retirement? – 30 years – another 360 payslips – it’s later than you think!
Related Article: